Библиотека численных методов для PascalABC.NET

Admin · 28.Июнь.2017 08:23:17

По-моему, массив из кортежей - это обычный массив

Почему?

  var a := Partition(1.0,2.0,10).Select(x->Point(x,f(x)));

RAlex · 28.Июнь.2017 08:34:25

Конечно же нет, я их вычислил для случая полинома пятой степени и синусоидальной функции при помощи этой же программы. Результат сплайн-интерполяции при помощи конкретной программы на бумаге не вычислишь: на то он и численный метод. Мы же не оцениваем результат, как отклонение от истинного значения, а проверяем, работает ли модуль, т.е. эти тесты - просто верификация факта, что в очередной версии PascalABC.NET библиотека “не развалилась”. Там даже если аналитически считать, мы сразу упираемся в: а) конечную точность вычисления значения функции б) конечную точность решения системы уравнений. А вот полином третьей степени - там именно вычисление функции сделано.

Т.е. Вы предлагаете сделать класс Point со своим конструктором, определить над ним набор операций и т.д.? Ведь давайте на минуту представим, что интерполяция - лишь часть задачи и исходные точки (может быть, отдельно их абсциссы даже) нужны также и в других целях. Делать Point.UnZip? И еще. Если график построить захочется, придется подключать GraphABC. А там Point уже есть…

RAlex · 28.Июнь.2017 09:09:37

А главное, я пока не увидел явной пользы от этого. Коды реализации численных методов это только усложнит. Практически там нет операторов, где одновременно используются абсцисса и ордината точки, а вместо x[i] и y[i] придется писать что-то в стиле P[i][0] и P[i][1]? При этом резко рушится информативность кода. А если сделать свойства и писать P[i].x, P[i].y, то вроде и кортеж непонятно зачем, а код просто получается длиннее. Можно, конечно, принимать параметры массивом кортежей и тут же рассыпать его в два одномерных массива х и у, но это лишь двойной расход памяти. Может, я чего-то не понял, просветите.

Admin · 28.Июнь.2017 10:08:07

Нет, это неправильно, функцию проверять этой же функцией. Проинтерполируйте известную во всех точках аналитическую функцию.

Нет. Тесты - это иллюстрация того факта, что написанная программа - правильная

А Вы вычислите с точностью 0.1. Просто если там 0, а будет считаться 1000, это не очень.

Да, именно это. Можно просто

type Point = auto class
public
  x,y: real;
end;

Нормальная запись вроде

Ну не знаю честно говоря. Вы разработчик. Я уже давно не программировал численные методы. Просто 2 массива - это мне не нравится, а массив точек для интерполяции - это как-то естественно. А если точки потребуются для чего-то ещё - тут-то Вы их и преобразуете. В PascalABC.NET для этого все средства есть

RAlex · 28.Июнь.2017 11:40:29

К сожалению, с автоклассом у меня получается только так: var pp := Partition(1.0,10.0,10).Select(x->new Point(x,x*x*x)).ToArray;

RAlex · 28.Июнь.2017 14:29:12

На текущей стадии вышло вот так (там уже две программы в библиотеке):

Summary

uses StudLib;

procedure TestSpline(x:real; F:real->real; eps:real; S:Spline);
// eps - абсолютная погрешность в процентах
begin
  var r1:=F(x);
  var r2:=S.Value(x);
  var Msg:='F('+x+')='+r1+', получено '+r2;
  Assert(Abs((r1-r2)/r1)<=eps/100,Msg);
end;

procedure TestZeroin(s:string; a,b:real; F:real->real; root,eps:real);
// root - точное значение корня
// eps - относительная погрешность значения корня
begin
  var x:=Zeroin(a,b,F,eps);
  var Msg:=s+': корень: '+x+', ожидалось '+root;
  Assert(Abs(x-root)<=eps,Msg);
end;

begin
  
  var f:real->real:=x->x*x*x;
  var pp:=Partition(1.0,10.0,9).Select(x->new Point(x,f(x))).ToArray;
  var Sp:=new Spline(pp); // создаем сплайн с заданными узлами интерполяции.
  TestSpline(1,f,1e-15,Sp); // левая точка
  TestSpline(1.25,f,1e-15,Sp); // внутри
  TestSpline(2.5,f,1e-15,Sp); // внутри
  TestSpline(7.2,f,1e-15,Sp); // внутри
  TestSpline(10,f,1e-5,Sp); // правая точка
  //
  f:=x->Power(x,4);
  pp:=Partition(1.0,10.0,9).Select(x->new Point(x,f(x))).ToArray;
  Sp:=new Spline(pp);
  TestSpline(1.28,f,32,Sp); // 32% у края... надо исходный шаг мельче
  TestSpline(2.5,f,0.8,Sp); // 0.8%
  TestSpline(5.1,f,0.005,Sp); // 0.005%
  TestSpline(9.7,f,0.01,Sp); // 0.01%
  //
  pp:=Partition(1.0,10.0,36).Select(x->new Point(x,f(x))).ToArray;
  Sp:=new Spline(pp);
  TestSpline(1.28,f,0.03,Sp); // 0.03%
  TestSpline(1.1,f,0.24,Sp); // 0.24%
  TestSpline(1.03,f,0.18,Sp); // 0.18%
  //
  f:=x->(3*x-8)/(8*x-4.1);
  pp:=Partition(1.0,10.0,18).Select(x->new Point(x,f(x))).ToArray;
  Sp:=new Spline(pp);
  TestSpline(1.1,f,4.8,Sp); // 4.8%
  TestSpline(2.6,f,5.8,Sp); // 5.8%
  TestSpline(5.9,f,0.001,Sp); // <0.001%
  TestSpline(9.9,f,0.001,Sp); // <0.001% 
  //
  Writeln('Проверка Spline завершена');
  //
  f:=x->x*(x*x-2)-5; // классика
  // Точное решeние по формуле Кардано 2.094551481542326591482386540579...
  var root:=(Power(5+Sqrt(643/27),1/3)+Power(5-Sqrt(643/27),1/3))/Power(2,1/3);
  TestZeroin('Zeroin1',2,3,f,root,1e-15);
  //
  f:=x->Power((12-2*x)/(x-1),1/3)+Power((x-1)/(12-2*x),1/3)-2.5;
  root:=2;
  TestZeroin('Zeroin2',1.01,3.5,f,root,1e-15); // разрыв при х=1
  //
  root:=97/17;
  TestZeroin('Zeroin3',3,5.99,f,root,1e-15); // разрыв при х=6
  //
  f:=x->3*Sin(x)+4*Cos(x)-5;
  root:=2*ArcTan(1/3);
  TestZeroin('Zeroin4',-1,1,f,root,1e-8);
  //
  Writeln('Проверка Zeroin завершена')
  //
end.

StudLib.pas (4,2 КБ)

Может, пора отдельную ветку делать?

RAlex · 28.Июнь.2017 19:21:18

Кстати, замечания и предложения по составу и интерфейсам принимаются от всех желающих с благодарностью.

spectatorBH · 28.Июнь.2017 21:35:26

procedure TestSpline(x:real; F:real->real; eps:real; S:Spline);
// eps - абсолютная(?) погрешность в процентах
...
Assert(Abs((r1-r2)/r1)<=eps/100,Msg);

Здесь как раз eps у вас выступает как относительная погрешность в процентах (по модулю), а вот тут:

procedure TestZeroin(s:string; a,b:real; F:real->real; root,eps:real);
// root - точное значение корня
// eps - относительная(?) погрешность значения корня
...
Assert(Abs(x-root)<=eps,Msg);

…напротив, уже вычисляется как абсолютная погрешность значения (по модулю).

RAlex · 28.Июнь.2017 21:42:36

Спасибо, что заметили, на самом деле там были другие формулы, переиграл, а комментарий не поправил

RAlex · 29.Июнь.2017 14:05:58

На данное время библиотека содержит три численных метода:

интерполяция табличной функции кубическим сплайном Spline;
отыскание корня уравнения на заданном интервале изоляции Zeroin;
адаптивная квадратурная программа для вычисления определенного интеграла Quanc8

Примеры вызовов находятся в тестирующей программе StudLibTest. StudLib.pas (7,9 КБ) StudLibTest.pas (4,0 КБ)

RAlex · 30.Июнь.2017 11:49:40

Библиотека пополнена и в данное время содержит 4 численных метода:

интерполяция табличной функции кубическим сплайном Spline;
отыскание корня уравнения на заданном интервале изоляции Zeroin;
адаптивная квадратурная программа для вычисления определенного интеграла Quanc8;
поиск минимума функции одной переменной на заданном интервале FMin

Примеры вызовов находятся в тестирующей программе StudLibTest. StudLib.pas (10,0 КБ) StudLibTest.pas (4,6 КБ)

RAlex · 02.Июль.2017 14:44:13

Библиотека пополнена и содержит 5 численных методов:

интерполяция табличной функции кубическим сплайном Spline;
отыскание корня уравнения на заданном интервале изоляции Zeroin;
адаптивная квадратурная программа для вычисления определенного интеграла Quanc8;
поиск минимума функции одной переменной на заданном интервале FMin
нахождение всех корней полинома степени не выше 36 с действительными коэффициентами
методом Ньютона - Рафсона (PolRT).

Примеры вызовов находятся в тестирующей программе StudLibTest. StudLib.pas (13,1 КБ) StudLibTest.pas (6,5 КБ)

RAlex · 02.Июль.2017 15:07:10

И еще раз к вопросу о том, не проще ди подключиться к готовой библиотеке через какой-то интерфейс. Вот заголовок подпрограммы DPOLRT, как она дана в SSP:

      SUBROUTINE DPOLRT(XCOF,COF,M,ROOTR,ROOTI,IER)
      DIMENSION XCOF(1),COF(1),ROOTR(1),ROOTI(1)
      DOUBLE PRECISION XCOF,COF,ROOTR,ROOTI,XO,YO,X,Y,XPR,YPR,UX,UY,V,
     1YT,XT,U,XT2,YT2,SUMSQ,DX,DY,TEMP,ALPHA

А вот пример вызова:

После портирования интерфейс выглядит намного проще и пользоваться им намного удобнее:

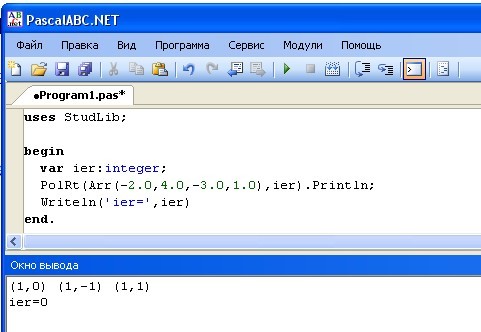
function PolRt(xcof:array of real; var ier:integer):array of complex;

Пример вызова:

var xcof:=Arr(-120.0,34.0,-4.0,-1.0,1.0);
var ier:integer;
var r:=PolRt(xcof,ier);
if ier=0 then r.Println
else Println('ier=',ier)

а если ier проверять не требуется, то просто PolRt(xcof,ier).Println;

Admin · 02.Июль.2017 18:33:44

Я говорю про более современные библиотеки численных методов. Я не владею вопросом - может, их нет. Но как-то странно, по всему есть, а по численным нет…

RAlex · 02.Июль.2017 19:25:29

Есть. Например вот - огромная платная библиотека.

Это прекрасная библиотека. Но… очень большая. Очень. В 2001 году по ней О.В. Бартеньев выпустил книгу (точнее, три отдельных тома объемом по 300-400 страниц каждый). Но уже 16 лет прошло…

Посмотрим, как с помощью IMSL нейти корни полинома.

Мы же теперь (причем бесплатно!) легко делаем то же самое за одну-две минуты:

…PascalABC.NET - замечательная дверца во взрослый мир программирования. Его возникновение и существование не преследовало и не преследует цели на мировое господство среди прочих языков и технологий программирования. Ничего плохого не будет, если установив на компьютер PascalABC.NET, человек получит заодно и возможность поучиться использовать готовые библиотеки, реализующие наиболее частые и понятные задачи. Делая самостоятельные задания по численным методом, можно посмотреть исходный текст, как пример реализации, можно написать свои программы и протестировать их готовыми тестовыми наборами… Вот такой смысл этой затеи, а вовсе не подмена “взрослых” промышленных библиотек и готовых математических пакетов…

RAlex · 03.Июль.2017 05:17:15

А вот так, к примеру, предлагает решать проблему нахождения корней полинома НИВЦ МГУ Я довольно долго разбирался, как с этим работать))) А начинать работу надо отсюда В целом - не рекомендую: паскалевская реализация под Дельфи предполагает множественную правку, надо переделывать весь ввод-вывод, разбросанный по модулям, часть математических функций отсутствует и должна заменяться на аналогичные из System.Math. Есть просто ошибки, когда объявляются константные массивы, а потом передаются как var в процедуры - они плохо диагностируются, потому что получаем сообщение про “неправильные” параметры при вызове процедуры Не помню точный текст. В общем, работка не для слабонервных и требующая знания особенностей Дельфи.

Вот еще одна из веточек форума, где участники делятся своими мытарствами по поводу работы с существующими библиотеками.

Конечно, когда в учебном заведении или в организации установлен какой-то пакет стандартных программ и есть методические наработки по его использованию, это отлично. Но если речь о лице, занимающемся самообразованием, о школе, лицее, колледже, небольшом филиале вуза - на первых порах готовая бесплатная библиотека численных методов с открытым кодом вполне может принести пользу.

RAlex · 03.Июль.2017 07:05:36

Отсюда можно взять неплохое учебное пособие формата PDF по численным методам, где разбираются примеры работы с программами из книги Дж.Форсайта, которые были (и еще будут) мной портированы с фортрана. В Приложении П5.2 предлагаются варианты готовых лабораторных работ по численным методам на базе упомянутых программ.

П5.2. Лабораторные работы П5.2.1. Интерполяция и квадратурные формулы (программы SPLINE, SEVAL, QUANC8) П5.2.2. Решение систем линейных алгебраических уравнений(программы DECOMP и SOLVE) П5.2.3. Решение систем обыкновенных дифференциальных уравнений (программа RKF45)

Саму книгу Форсайт Дж., Малькольм М., Моулер К, “Машинные методы математических вычислений” можно взять здесь .

RAlex · 03.Июль.2017 21:13:25

Библиотека пополнена и содержит 6 численных методов:

интерполяция табличной функции кубическим сплайном (Spline);
отыскание корня уравнения на заданном интервале изоляции (Zeroin);
адаптивная квадратурная программа для вычисления определенного интеграла (Quanc8);
поиск минимума функции одной переменной на заданном интервале (FMin)
нахождение всех корней полинома степени не выше 36 с действительными коэффициентами методом Ньютона - Рафсона (PolRT)
решение систем линейных уравнений путем LU-разложения методом Гаусса (Decomp/Solve)

Примеры вызовов находятся в тестирующей программе StudLibTest. StudLib.pas (16,2 КБ) StudLibTest.pas (9,1 КБ)

ibond · 04.Июль.2017 17:47:53

если б еще функция Polynom(‘z^3-3z^2+4z-2’) была, то было бы совсем замечательно…

Admin · 04.Июль.2017 18:55:18

Представляю, сколько ошибок можно совершить в написании ‘z^3-3z^2+4z-2’ :))