Д.з. - языки программирования, возникшие за последние 10 лет (про распространенность ничего сказано не было)
2008 год Objeck — объектно-ориентированный язык с некоторыми функциональными элементами (функции высшего порядка). Прототип языка был создан для исследования процесса трансляции команд стека в команды регистра и затем в машинные коды. По этому прототипу была создана виртуальная машина с простым ассемблером. Со временем ассемблер был заменен на гораздо более сложный объектно-ориентированный фронт-энд, и проект был переименован в Objeck. В настоящее время язык считается стабильным, и его развитие фокусируется на дальнейшем упрощении программирования. Язык не проходил стандартизацию, и авторская реализация остается единственной. В нее входят компилятор (в байт-код), виртуальная машина со сборщиком мусора и динамическим компилятором и отладчик с интерфейсом командной строки. Все типы данных, за исключением функций высшего порядка, считаются объектами.


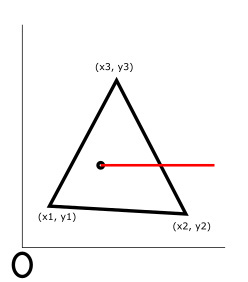 . Таким образом, я сравнивал сначала, лежит ли Ум между ординатами отрезков, а потом лежит “слева” или “справа” от отрезка с помощью хитрых формул. Создавал отдельную функцию, подобную Between, но с одним нестрогим сравнением. Необходимо было для обработки случаев, когда луч пересекал вершину. Единственное исключение, которое надо было отдельно обработать - когда луч совпадает с какой-то из сторон. Т.е. когда отрезок параллелен ОХ, а так же точка лежит на этой стороне. Жду комментариев от других, явно, что мой код не идеален.
. Таким образом, я сравнивал сначала, лежит ли Ум между ординатами отрезков, а потом лежит “слева” или “справа” от отрезка с помощью хитрых формул. Создавал отдельную функцию, подобную Between, но с одним нестрогим сравнением. Необходимо было для обработки случаев, когда луч пересекал вершину. Единственное исключение, которое надо было отдельно обработать - когда луч совпадает с какой-то из сторон. Т.е. когда отрезок параллелен ОХ, а так же точка лежит на этой стороне. Жду комментариев от других, явно, что мой код не идеален. Институт математики, механики и компьютерных наук ЮФУ, 2005–2021
Институт математики, механики и компьютерных наук ЮФУ, 2005–2021